Welcome!

My name is Xandru Mifsud, a current DPhil student in Computer Science at the University of Oxford, as a Clarendon Scholar, under the supervision of Leslie Ann Goldberg and Andreas Galanis.
Previously, I attained an M.Sc. in Mathematics from the University of Malta (supervised by Josef Lauri, Christina Zarb and Yair Caro).
My main research interests are combinatorics, (randomised) algorithms, and their intersection.
Over the past three years, I have also tutored and lectured a number of units at the Department of Computer Science within the University of Malta. For a detailed look at my work in and out of academia, kindly view my curriculum-vitae.
My Erdős number is 3, by the chains X. Mifsud → J. Lauri → F. Harary → P. Erdős, and X. Mifsud → Y. Caro → N. Alon → P. Erdős.
Research
Pre-prints
[1] Y. Caro and X. Mifsud, "On zero-sum Ramsey numbers modulo 3", (submitted, 2025), pre-print available at: https://arxiv.org/pdf/2502.03864.pdf
Papers
[5] X. Mifsud, "Flip colouring of graphs II", Bulletin of the Institute of Combinatorics and its Applications (to appear), pre-print available at: https://arxiv.org/pdf/2401.02315.pdf
[4] Y. Caro, J. Lauri, X. Mifsud, R. Yuster and C. Zarb, "Flip colouring of graphs", Graphs and Combinatorics (2024), available at: https://doi.org/10.1007/s00373-024-02838-w
[3] Y. Caro and X. Mifsud, "On $(r,c)$-constant, planar and circulant graphs", Discussiones Mathematicae Graph Theory (2024), available at: https://doi.org/10.7151/dmgt.2551
[2] X. Mifsud, "λ-Core Distance Partitions", Linear Algebra and Its Applications (2021), available at: https://doi.org/10.1016/j.laa.2020.12.012
[1] I. Sciriha, X. Mifsud and J. L. Borg, "Nullspace vertex partition in graphs", Journal of Combinatorial Optimization (2020), available at: https://doi.org/10.1007/s10878-020-00624-x
Notes / Tool Papers
[2] X. Mifsud and S. Spina, "A Streamable SAT Framework for the Parallel Algorithmic Lovász Local Lemma", in preparation (tool paper) (2024)
[1] X. Mifsud, "A lower-bound for the number of conjugacy classes of $A_n$", 2023, available at: https://arxiv.org/pdf/2310.12047.pdf
Talks
[5] Constructing (small) $(b,r)$-flip graphs, Open University Discrete Mathematics Seminar, 6th November 2024.
[4] On $(r,c)$-Constant Circulants, 30th British Combinatorial Conference (QMUL), 1st July 2024. Talk on joint work with Yair Caro. View the slides here.
[3] Local v. Global Majority: An Edge-Colouring Approach, University of Malta, 23rd May 2024. Talk given about my masters project, supervised by Josef Lauri, Christina Zarb, and Yair Caro. View the slides here.
[2] Hamiltonicity of Cayley Graphs and Digraphs, University of Malta, 19th May 2022. Talk given about my undergraduate project, supervised by Josef Lauri. View the slides here.
[1] Nullity Relations on Graphs with Independent Core Vertices, University of Malta, 31st January 2019. Talk given for Graph Theory and Combinatorics Day. View the slides here.
Visualising Graph Spectra
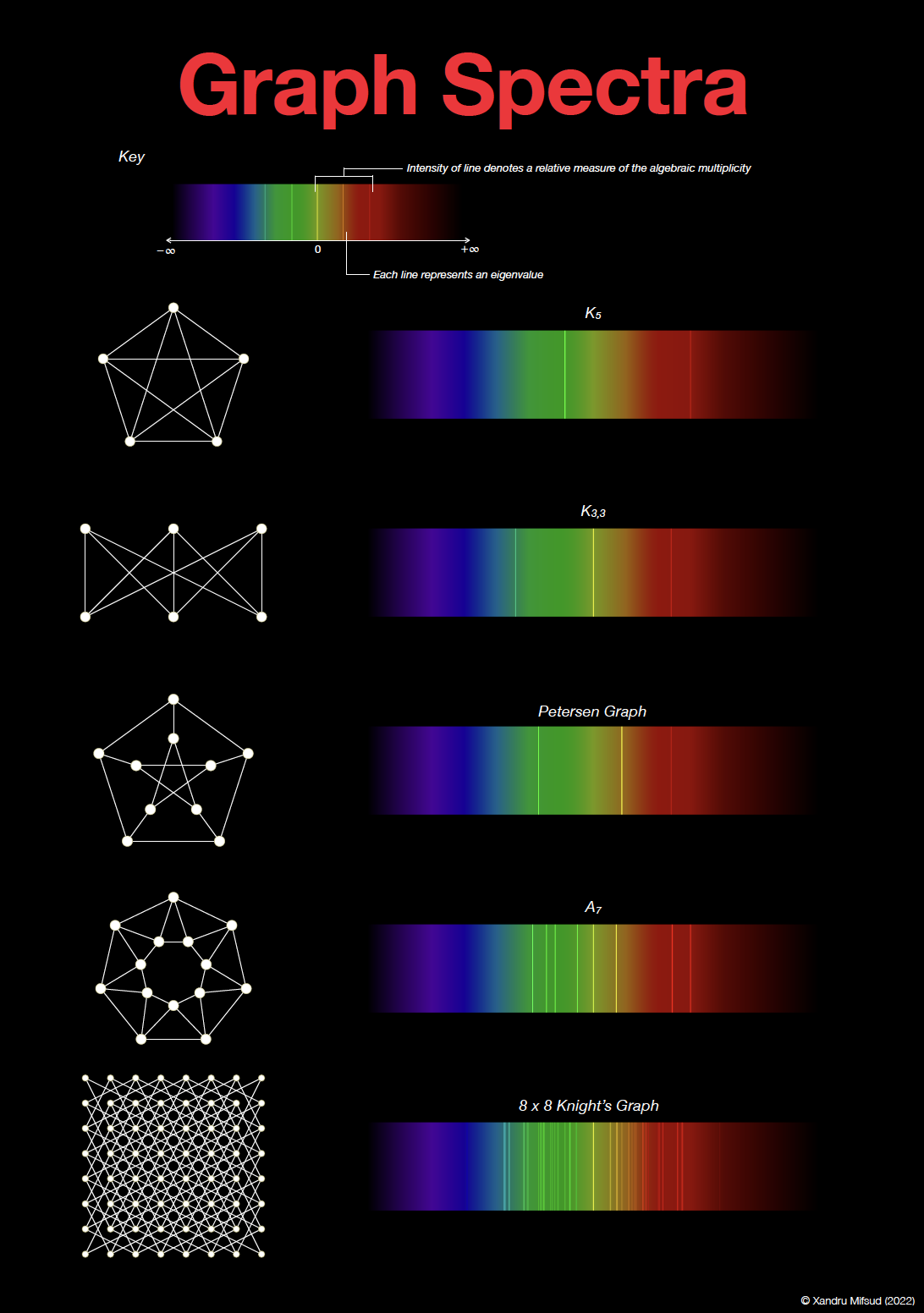
The eigenvalues of the adjacency matrix of a graph form a `finger print` of the graph, what mathematicians term as the spectrum of the graph. Physicists and chemists may be reminded of emission spectra, and the beautiful visualisations one obtains through the use of a spectrometer.
The poster on the left is the product of a small project I developed, tying in these two aspects together - along with, in my opinion, art. Click on the image to download the poster in high resolution. And click here to download a Mathematica notebook which aids one in visualising the spectrum of their favourite graph.
Cauchy's Interlacing Theorem states that if $\lambda_1 \geq \lambda_2 \geq \dots \geq \lambda_n$ are the eigenvalues of a graph, and $\mu_1 \geq \mu_2 \geq \dots \geq \mu_{n-1}$ are the eigenvalues of a vertex-deleted subgraph, then
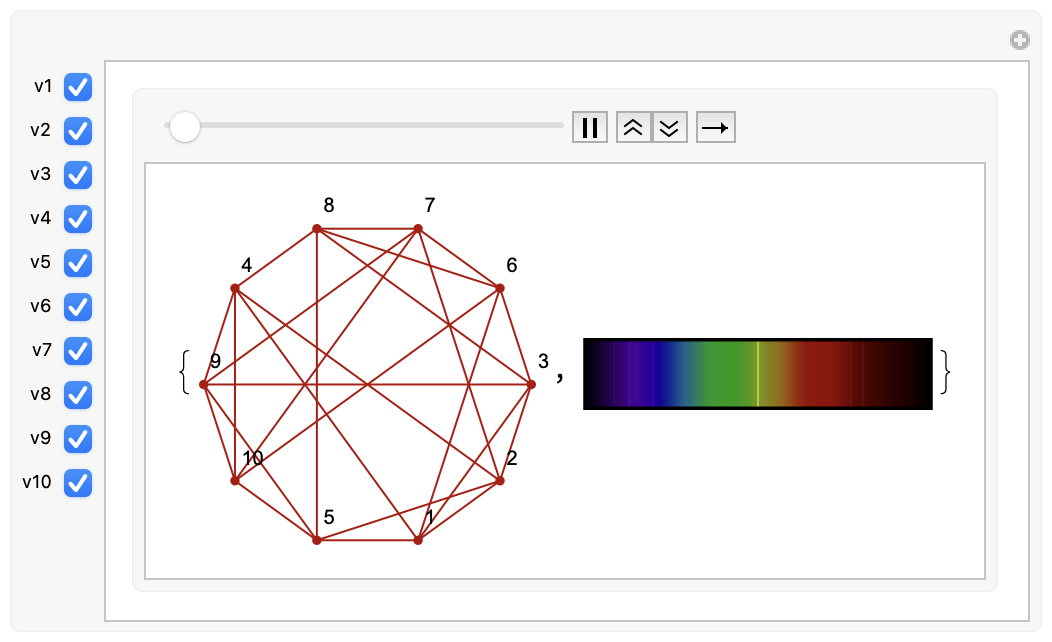
$\lambda_1 \geq \mu_1 \geq \lambda_2 \geq \dots \geq \mu_{n-1} \geq \lambda_n$
ie. the eigenvalues interlace. The Mathematica notebook includes a visual example (imaged on the right) of this theorem. Simply uncheck one or more vertices (to represent deletion), and drag the slider. Observe how the spectral lines interlace as you drag the slider.
Historical Notes on Mathematics in Malta
(Supervision) Genealogy of the Department of Mathematics, University of Malta.
All content, unless otherwise stated, on this site is © Xandru Mifsud (2025).